Prekidačka algebra – Boole-ova algebra – Algebra logike
5. Minimizacija prekidačkih funkcija

5.4 Karnoova (Karnaugh) metoda minimizacije - Treći primjer

Treći primjer: neka je data funkcija

Karnoova tablica za ovu funkciju izgleda ovako

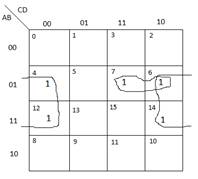
Imamo jednu površinu drugog reda koju čine polja  i jednu površinu prvog reda koju čine polja . Na osnovu označenih skupova polja koja čine zajedničke površine dobija se minimizirani oblik funkcije

Gornja funkcija može se prikazati i proizvodom zbirova (POS forma)

koji su unijeti u K-tablicu na sljedećoj slici

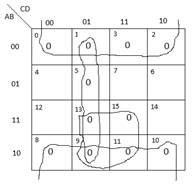
Formirajući odgovarajuće površine (skupove polja), iz tablice se dobija minimizirana funkcija

Primjećujemo da ovdje imamo jednu površinu trećeg reda (8 polja) i dvije površine drugog reda (4 polja). Podsjetimo da su logičke sume u POS normalnoj formi funkcije definisane za vrijednost 0, pa su zato u tablicu upisane nule.
Razumljivo je da dobijene minimizirane funkcije u SOP i POS formi moraju biti iste, što se i pokazuje transformacijom posljednje funkcije

Karnoova (Karnaugh) metoda minimizacije - Drugi primjer    <    Index    >    Operacije ILI, I i NE