Prvi tip zadataka koji se javljaju kod problema sa limesima jesu zadaci kod kojih moramo da koristimo racionalizaciju.

Zadatak 1:

Ako bismo uvrstili x=1 dobili bismo nula kroz nula, a znamo da se ne može dijeliti sa nulom. Zato vršimo racionalizaciju:

Kada vidimo u zadatku nakon racionalisanja da postoje izrazi koji daju 0, i ako imamo šta da skratimo onda skraćujemo razlomak:

Kada dobijemo izraze u razlomku koji su mogući kada uvrstimo x=1, tj. kada ne dobijamo 0, uvrštavamo x i dobijamo konačan rezultat:

Zadatak 2: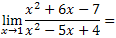

Ovaj zadatak radimo na sličan način kao i prethodni. Dakle prvo racionalizacija, sve dok prilikom uvršavanja broja kojem x teži ne dobijemo konačan rezultat.

Drugi tip zadataka su zadaci prilikom čije izrade koristimo limese do kojih smo došli eksperimentalno.

Prve ćemo izdvojiti .

Zadatak 1:

Vrijednost ovog limesa je , zato nastavljamo dalje dok ne dobijemo konačan rezultat. Najjednostavniji način izrade je ako izvučemo x ispred zagrade, ili podijelimo i brojilac i imenilac sa x:

(Izraz 1/x ima vrijednost 0, tako da je rezultat ovog zadatka 1.)

Zadatak 2:

I ovaj zadatak radimo na isti način kao i predhodni, dakle izvući ćemo x ispred zagrade s cilje da dobijemo n/x i tako riješimo zadatak:

Sljedeći limes do kojeg smo došli eksperimentalno je .

Zadatak 1:

Ovaj zadatak ćemo uraditi tako što ćemo i brojilac i imenilac pomnožiti sa 4 da bismo dobili odgovarajuću vrijednost x i gore i dole:

Kada smo dodali 4 i gore i dole prepoznali smo koje je eksperimentalni limes i ima vrijednost 1. I ostala nam je 4.

Zadatak 2:

Važno je napomenuti da zadaci kao što je ovaj zahtijevaju poznavanje trigonometrijskih funkcija.

Zadatak 3:

Ovdje ćemo prvo uvesti smjenu: , pa kad , onda , dakle .

(Prema trig. formulama )

Sljedeći limesi do kojih smo došli eksperimentalno su: i .

Zadatak 1:

Ovdje gdje je 3 mora biti 1, tako da ćemo 3 "spustiti" ispod x.

Sljedeći korak je da kod x u eksponentu pomnožimo i podijelimo sa 3.

Zadatak 2:

Da bismo sebi olakšali u zagradi ćemo dodati i oduzeti 1.

Određivanje asimptota

Zadatak 1: Odrediti asimptote funkcije .

Prvo ćemo odrediti vertikalnu asimptotu, ali prije toga moramo da odredimo domen ove funkcije.

Vertikalna asimptota postoji ako postoji tačka u kojoj funkcija nije definisana. A mogu da postoje i više tačaka u kojima funkcija nije definisana.

Ako posmatramo našu funkciju , ona nije definisana kada je x=2. I zato ćemo ispitati njeno ponašanje u okolini ove tačke.Prvo ćemo posmatrati ovu tačku kada joj se približavamo sa lijeve strane, a to zapisujemo 2-0 ili 2-.

Sada ćemo ispitati njeno ponašanje kada joj se približavamo sa desne strane, a to zapisujemo 2+0 ili 2+.

I naš zaključak je da funkcija ima vertikalnu asimptotu x=2.

Sljedeći korak je da ispitamo ima li naša funkcija kosu asimptotu. Ako nema kosa, onda postoji horizontalna.

Opšta formula kose asimptote je y=kx+n.

Formula za k je: , a za n:.

Vrijednost k koje smo dobili koristimo pri računanju n.

I dobili smo da kosa asimptota glasi y=x-3

• Kako ćemo znati kada nema kose asimptote, a postoji horizontalna?

Znaćemo ako prilikom računanja nemamo k, a imamo n. Onda je horizontalna asimptota y=n. Najlakše nam je da prvo pronađemo vertikalnu asimptotu, ako postoji, te tražimo kosu asimptotu. Ako kosa asimptota nema k, a ima n, onda imamo horizontalnu. Funkcija ne može da ima i horizontalnu i kosu asimptotu u isto vrijeme.

Lopitalovo pravilo

Da bismo koristili ovo pravilo, neophodno je poznavanje tablice izvoda. Ako nju znamo, nećemo imati problema sa ovim zadacima.

Zadatak 1:

Ovaj eksperimentalni limes lako ćemo izraćunati pomoću Lopitalovog pravila.

Zadatak 2:

Kod ovog zadatka ćemo morati da koristimo Lopitalovo pravilo dva puta. Ali mi možemo da koristimo ovo pravilo dok god ne prestanemo da dobijamo neodređene oblike ili .