EKSPERIMENTALNI DIO

OSCILACIJE

            Pojam oscilacije je pojam vremenskih promjena polozaja u jednoj, fiksnoj tacki prostora pod djelovanjem neke sile. Definisemo neku elasticnu silu i u njenom polju opišimo slobodne ili harmonicke oscilacije.

                Polozimo li os x u smijeru djelovanja elasticne sile mozemo je napisati i u skalarnom obliku:

gdje je k=m wo2 konstanta elasticne sile.

II Newtonov princip nam daje:

što nakon sredivanja i dijeljenja sa m definira diferencijalnu jednacinu harmonickog oscilatora:

            Pretpostavimo rješenje u obliku  x=ert , što nam uvrštavanjem daje:

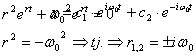
pa imamo dva partikularna rješenja:

            Uzevši Eulerov obrazac e±if = cosf  ± i sinf

            Redefinisimo konstante

i osnovna trigonometrijska relacija nam daje konacno rješenje.

gdje je A amplituda oscilacija, ( wot +  fo) faza oscilacija i  fo pocetna faza.

            Definisimo period oscilacije kao vrijeme potrebno da se oscilacija vrati u pocetni polozaj.

gdje je  kruzna frekvencija oscilacije a   n = 1/T je frekvencija oscilacija.

            Energija oscilacije E = ½ m  wo2 × A2

ODREDIVANJE UBRZANJA ZEMLJINE SILE TEZE

            MATEMATICKO KLATNO

            Matematicko klatno je jednostavni sistem harmonijskog oscilovanja. To je tijelo obješeno na tanak neistezljiv konac cije su dimenzije male u odnosu na duzinu konca. Tezina klatna mg se razlaze na dvije komponente:Fk koja zateze konac i u revnotezi je sa otporom konca –Fk i Fg koja je normala na Fk i tangencijalna na luk OA. Pod djelovanjem Fg kuglica se ubrzava dobivajuci kineticku energiju. Uslijed stecene kineticke energije klatno se ne zaustavlja u ravnoteznom polozaju 0 vec nastavlja kretanje sve dok se kineticka energija ne pretvori u potencijalnu. Naime, kada klatno dospije u tacku B, kuglica se u odnosu na tacku 0 podigne za iznos h i stegne potencijalnu energiju mgh. U tocki B kuglica se zaustavi i onda ponovo pod djelovanjem Fg koja je sada usmjerena suprotno pocinje kretanje unazad pretvarajuci potencijalnu energiju u kineticku. I tako izmjenicno kretanje se periodicno ponavlja po istoj putanji. Vrijeme potrebno da kuglica iz A dode u B i vrati se natrag u B je period kretanja T. Sa slike 1. Je ocigledno da su kutovi  i ANP jednaki. Stoga je Fg = -mg sin  = -mg sin x/L                       =x/L.

Znak “ - “ izrazava bitno vazno svojstvo sile Fg naime, to znaci da je sila usmjerena u preotivnom smijeru povecanja kuta.

            Nadalje pretpostavimo da klatno osciluje sa vrlo malim uglovima. Tada vrijedi:  sin      x/L  i izraz konacno prelazi u Fg = - mg x/L. buduci da su L i g konstante, ocigledno je da Fg predstavlja kvazielasticnu silu jer linearno zavisi od puta x. Jasno je onda da pod djelovanjem sile Fg klatno vrši harmonicke oscilacije pod zanemarenim otporom zraka i trenjem u objesištu.

            Na osnovu drugog Newtonovog zakona pišemo

Poredjenjem toga sa opcom jednacinom harmonickih oscilacija jasno je   2 = g/L

            Kako je   = 2   = 2  /T  dobijamo lako izraz za period oscilacija

            Ocigledno je da period malih oscilacija periodickog klatna ne ovisi od mase klatna i amplitudi oscilacija. Opste rješenje jednacine je:   x = xo sin ( t +  ), gdje je xo mala amplituda oscilacija a  pocetna faza oscilacija za t = 0.

            Postupak pri mjerenju Pribor za mjerenje cine:

1.      Zaporna ura

2.      Zeljezna kuglica

3.      Tanka nit o koju je obješena kuglica

4.      Mjerilo za mjerenje duzine klatna

Za mjerenje duzine klatna treba vrh klizaca mjerila postaviti tako da tangira kuglicu. Ako je za slucaj tangiranja gornje strane kuglica ocitana duzina L1 a donje L2 tada je duzina L = (L1+L2)/2

            Uzmemo u ruku zapornu uru i izvedemo klatno iz ravnoteznog polozaja za malu elongaciju (1-2 cm) i pratimo osciliranje. Brojenje cijelih oscilacija vršimo u trenucima postizanja desne amplitude. Odbrojimo N punih oscilacija. Neka je  vrijeme izmjereno zapornom urom, onda je period T =  /N. Mjerenje se vrši za nekoliko razlicitih duzina. Rješavanjem jednacine (*) dobivamo relaciju:

U koju uvrštavamo odgovarajuce vrijednosti L i T i izracunamo g. Vrijednosti svrstavamo u sljedecu tablicu.  

Povratak