Mesopotamija, područje oko i između Eufrata i Tigra, bila je kolijevka jedne od, ili, možda bolje rečeno nekoliko najstarijih kultura. Govoreći o matematici stare Mesopotamije podrazumijevamo ostavštinu Sumeranaca, Vavilonaca, Asiraca, Akađana, Kaldejaca i drugih naroda koji su u pojedinim razdobljima živjeli na dijelovima tog područja. Takođe se često izraz "vavilonski" koristi kao sinonim za "mesopotamski". Većina najranijih civilizacija nastale su uz velike rijeke koje su omogućile navodnjavanje i time razvoj poljoprivrede, kao i plovidbu. Na taj način bi se povezala naselja u cjeline koje su razvijale svoju kulturu i civilizaciju.

 

Mnogo stotina tablica u klinastom pismu bavi se problemima koje bismo danas nazvali algebarskim ili se bave geometrijskim odnosima. Nađeno je mnogo hiljada koje služe za računanje. Vavilonci su se služili tablicama kao što se mi danas služimo npr. logaritamskim tablicama. Među tablicama za množenje bile su tablice koje bismo mogli nazvati "tablicama recipročnih vrijednosti", pomoću kojih su Vavilonci dijeljenje mogli svoditi na množenje. Osim tih tablica, imali su i tablice za kvadrat i kub, te za drugi i treći korijen.

Nađene su i njihove tabliceza vrijednosti od n³ + n² u rasponu od n=1 do n=30, kojima su npr. mogli rješavati kubne jednačine oblika:  n³ + n² = a za zadano, poznato a i nepoznato n.

 

Vavilonska aritmetika je bila, relativno mjereno, visoko razvijena. Pojedini njihovi računi koji bi, sa obzirom na to da rade sa "konkretnim" brojevima, po našoj uobičajenoj klasifikaciji spadali u aritmetiku, zapravo su po svome duhu, po načinu na koji su formirani i vođeni, jasni dokazi da je tu riječ i o algebarskom mišljenju. Na primjer, jedna sumacija kvadrata prvih deset brojeva pokazuje da su Vavilonci znali kako treba postupiti da bi se dobio zbir kvadrata koliko god prirodnih brojeva, počevši od jedan redom dalje.

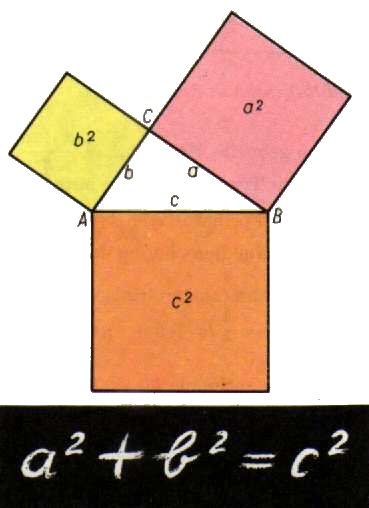
Što se geometrije tiče, obim kruga i obim kružnog valjka računa se u načelu tačno sa (u starije vrijeme) aproksimacijom 3 za broj π = (3 1/8) = 3.125 (pogreška samo oko 0.5%). Za Pitagorinu teoremu su svakako znali, i to u njenom opštem obliku. Na po jednoj pločici staroj između tri i po i četiri hiljade godina gotovo je sigurno da su znali čak i za parametarsko predočenje Pitagorinih trojki brojeva, tj. brojeva a, b, c sa svojstvom da je a² + b² = a,tj. za predočenje tih brojeva u obliku: a=2uv, b=u²-v², c=u²+v².