

*UVOD
Jedna od najranijih kultura i civilizacija koje je čovjek stvorio na Zemlji, bila je staroegipatska. I danas ćemo se još uvijek ponovo zadiviti pred ostacima te velike baštine, razasutim po muzejima svijeta i u svojoj zemlji: bilo da je riječ o umjetničkim djelima u muzeju u Kairu, bilo da posmatramo ostatke čudesne građevine kraljice Hatšepsut, njenog hrama u Der el Bahariju, ili velikih piramida, hrama u Luksoru ili grobnica u Dolini kraljeva, bilo da čitamo šifrirane tekstove staroegipatske Knjige mrtvih... U svakom ćemo slučaju ostati iznenađeni pred snagom duha i volje i pred dubinom misli što su nikle i razvile se u dolini Nila prije nekoliko hiljada godina.
I staroegipatska matematika je jedna od najranijih epoha razvoja te nauke. Posebno jedna od prvih grana matematike - geometrija, već samim svojim nazivom otkriva i svoje porijeklo. To je po postanku grčka riječ koja bi, doslovno prevedena, značila "mjerenje zemlje". A upravo kod mjerenja zemlje geometrija se široko razvila već u starom Egiptu. Izreka:"Egipat je dar Nila", dovoljno je poznata. Bez blatnjavih, žutih voda te rijeke koje su hiljadama godina natapale zemlju ne bi se razvila tako bogata civilizacija starog Egipta. No, poslije redovnih poplava Nila, svake bi se godine granice zemljišnih posjeda izbrisale i trebalo ih je ponovo odrediti - valjalo je, dakle, premjeravati zemljišta. Izgradnja veličanstvenih hramova, piramida, kipova, takođe je zahtijevala određena znanja iz geometrije.

*PAPIRUS
To je komplementna "studija o svim stvarima, pogled u unutrašnjost svega što postoji, saznanje o tamnim tajnama", kako piše na samom papirusu. Ahmesov papirus je zbirka tablica i vježbi, retorička u svojoj formi, koja je namijenjena uglavnom učenju matematike. Sadrži vježbe iz aritmetike, algebre, geometrije i raznih mjerenja. Moskovski papirus otkrio je 1893. godine V.S.Golenčiev. Dug je 6 m, širok 8 cm. Sadrži 25 problema, od kojih mnogi nisu čitljivi. Čuva se u Moskovskom muzeju.
.jpg)

*KAKO SU RAČUNALI?
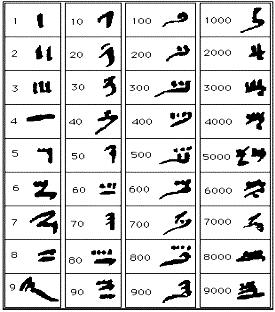
Stari egipćani su imali razvijen decimalni sistem i svoje oznake za brojeve (slika lijevo). Hijeroglifskim znakovima se pisalo po kamenu, kako s lijeva na desno, tako i obrnuto, a ponekad i odozgo prema dole. Različito pisanje ne stvara probleme kod čitanja brojeva jer egipatski način pisanja brojeva nije pozicijski. Hijeratički su znakovi uvedeni za brzo pisanje po papirusu, drvetu ili lončariji. Osim navedenih, povremeno su se upotrebljavali i neki posebni znakovi za brojeve koji nisu dekadne jedinice ( slika desno). Npr. za broj 2 crtali bi se goveđi rogovi, za broj 5 morska zvijezda, a ljudska glava je bila oznaka za broj 7.
Koristili su brojevni sistem sa bazom 10, a jedna od glavnih razlika između hijeratičkih brojeva i našeg brojevnog sistema jeste da hijeratički brojevi nisu bili pisani u sistemu mjesnih vrijednosti, tako da su brojevi mogli biti pisani bilo kojim redoslijedom. Hijeratički je sistem adicijski sistem. Vidimo da se, recimo, broj 249 zapisuje kao 249 = 2*100 + 4*10 + 9, pa u zapisu imaju dva znaka za 100, četiri znaka za 10 i devet znakova za 1.
Egipatski brojevni sistem nije bio pogodan za računanje, ali je trgovina zahtijevala sabiranje, oduzimanje, množenje, dijeljenje te rad sa razlomcima.

- SABIRANJE
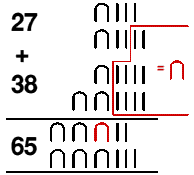

- ODUZIMANJE
Oduzimalo se tako što se odmicao određeni broj istih simbola. Ovo je znalo biti i komplikovano kad se moralo oduzeti više simbola nego što ih je bilo prisutno u prikazu.
Npr. evo kako bismo izračunali 63-38 (slika desno):
Od 6 desetica možemo oduzeti 3 desetice, ali možemo ukloniti samo 3 jedinice. Još nam preostaje 5 jedinica za oduzimanje. Jedna od preostalih desetica potrebna je da se omogući oduzimanje sljedećih 5 jedinica jer:
1 desetica - 5 jedinica = 10 jedinica - 5 jedinica = 5 jedinica.
Tačan mehanizam oduzimanja koji su oristili nije sasvim jasan, iako ova ilustracija pokazuje kojim je redoslijedom pisar mogao provesti oduzimanje.

- MNOŽENJE
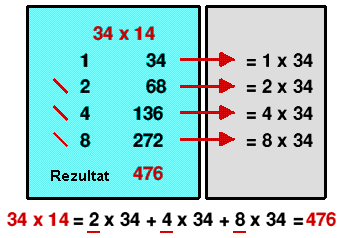
Množenje prirodnih brojeva odaje nam da su se služili i potencijama broja 2. Stari Egipćani množili su dva broja koristeći udvostručavanje brojeva (slika desno).
U plavom pravougaoniku prikazan je nihov zapis, a sivi pravougaonik i račun ispod pravougaonika objašnjavaju metodu: Broj su udvostručavali sabirajući ga samog sa sobom, dakle samo su zapisali brojeve jedan ispod drugog i pretvorili svakih 10 istih simbola u simbol sljedećeg nivoa. Kako nisu imali razvijen pozicijski zapis brojeva, moramo starim Egipćanima priznati veliku spretnost i ekonomičnost u računanju.
Kao što se vidi u tablici hijeroglifskih znakova, egipatski brojevni sistem je koristio simbole koji predstavljaju potencije broja 10 sa eksponentima od 0 do 6. I oni su uočili da je množenje broja 10 jednostavno: zamijenili bi svaki simbol onim susjednim po veličini, npr.: 236*10 = (6 jedinica postaje 6 desetica, 3 desetice postaju 3 stotine, 2 stotine postaju 2 hiljade) = 2 hiljade, 3 stotine i 6 desetica = 2360.
- DIJELJENJE
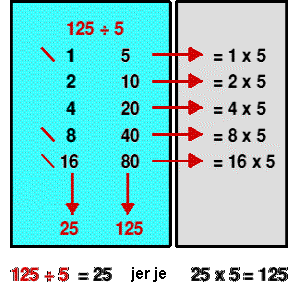
Dijeljenje starih Egipćana zahtijevalo je korištenje množenja i vrlo čestu upotrebu razlomaka. Prmjer djeljenja kada je rezultat cijeli broj (slika desno):
* 125 podijeljeno sa 5 daje isti rezultat kao 5 pomnoženo sa 25 = 125
* množi 5 uzastopno s višekratnicima od 2 sve dok ne dobiješ 125 (kao kod množenja
* zbir crveno označenih brojeva u plavom pravougaoniku daje rrješenje.
Ova metoda se temelji na jednostavnoj matematičkoj činjenici koja je bila poznata i egipatskim pisarima, a to je da su množenje i dijeljenje inverzne operacije, tj.: a*b = c, samo ako je c:b = a.
*GEOMETRIJA
Posmatrajući fantastične građevine koje su stari Egipćani ostavili u prilog svjetskoj bašini, ne možemo a da se ne zapitamo koliko su dobro imali razvijenu geometriju, stereometriju i sve ono što im je bilo potrebno za izgradnju piramida i hramova. Znamo da su znali računati nagib piramide, obim krnje piramide te obim piramide. Računali su površinu trougla kao 1/2 proizvoda dviju kraćih stranica (što vrijedi samo za pravougli trougao); mala odstupanja nisu im značila previše. Znali su izračunati i površinu pravougla kao proizvod dužina njegovih stranica.
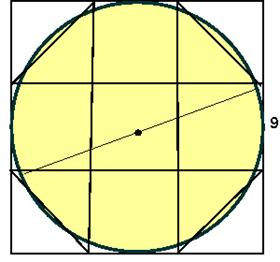
Ono što jeste fascinantno, a pronađeno je u Ahmesovom papirusu, je način na koji su računali površinu kruga:
* pretpostavimo da krug ima dijametar (prečnik) od 9 kheta (khet je jedinica za dužinu)
* uzmi 1/9 dijametra, dakle 1,
* ostatak je 8
* pomnoži 8 sa 8,
* dobiješ 64 i to je površina.

 |
 |
 |
 |
 |
 |