Programski jezik C++
Funkcije - Rekurzija /FUNCTIONS - RECURSION/ - Daljnji rad /NEXT/

Svi zadaci pogavalja (urađeni i neurađeni) prikazani su po grupama i redoslijedu.
Urađeni zadaci imaju link na rješenje.
Neriješeni zadaci su označeni sa Daljnji rad.

  I Funkcije - Rekurzija - 1-n /FUNCTIONS - RECURSION/ Rješenja
*** 1 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume prvih 5 brojeva.		  
2 Napisati rekurzivnu funkciju za izračunavanje sume prvih n brojeva. C++
3 Napisati rekurzivnu funkciju za izračunavanje sume kvadrata prvih n brojeva. C++
4 Napisati rekurzivnu funkciju za izračunavanje sume kubova prvih n brojeva. C++
*** 5 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume parnih od prvih n prirodnih brojeva.		  
*** 6 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume neparnih od prvih n prirodnih brojeva.		  
*** 7 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume djeljiih sa 3 od prvih n prirodnih brojeva.		  
8 Napisati rekurzivnu funkciju za izračunavanje sume prvih n neparnih prirodnih brojeva. C++
9 Napisati program sa rekurzijom za računanje proizvoda (faktorijela) prvih n brojeva. C++
10 Napisati rekurzivnu funkciju za izračunavanje proizvoda parnih od prvih n prirodnih brojeva. C++
*** 11 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje proizvoda neparnih od prvih n prirodnih brojeva.		  
*** 12 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje proizvoda djeljivih sa 3 od prvih n prirodnih brojeva.		  
*** 13 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje stepen broja 2 za vrijednosti eksponenta od 1 do 10.		  
14 Napisati rekurzivnu funkciju za izračunavanje izračunavanje n-tog stepena broja. C++
*** 15 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje aritmetičke sredine prvih pet prirodnih brojeva.		  
*** 16 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje aritmetičke sredine prirodnih brojeva od 1 do n.		  
  II Funkcije - Rekurzija - Opseg /FUNCTIONS - RECURSION - RANGE/ Rješenja
*** 17 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume prirodnih brojeva od 3 do 8.		  
*** 18 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume parnih u intervalu od 3 do 8.		  
*** 19 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume neparnih u intervalu od 3 do 8.		  
*** 20 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume prirodnih brojeva od k do n.		  
*** 21 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume prirodnih brojeva od a do b.		  
*** 22 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume kvadrata dvocifrenih brojeva.		  
*** 23 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume kvadrata prirodnih brojeva od k do n.		  
*** 24 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume kvadrata prirodnih brojeva od a do b.		  
*** 25 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume parnih u intervalu od k do n.		  
*** 26 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume neparnih u intervalu od k do n.		  
*** 27 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje sume dvocifrenih brojeva brojeva koji nisu djeljivi ni sa 2 ni sa 3.		  
*** 28 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje proizvoda prirodnih brojeva od 4 do 9.		  
*** 29 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje proizvoda parnih u intervalu od 2 do 8.		  
*** 30 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje proizvoda neparnih u intervalu od 4 do 7.		  
*** 31 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje proizvoda prirodnih brojeva od k do n.		  
*** 32 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje proizvoda parnih prirodnih brojeva od k do n.		  
*** 33 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje proizvoda neparnih prirodnih brojeva od k do n.		  
*** 34 Daljnji rad:
Napisati program za izračunavanje proizvoda prirodnih brojeva od a do b (koristiti rekurziju).		  
*** 35 Daljnji rad:
Napisati rekurzivnu funkciju za prebrojavanje prirodnih brojeva od 2 do 7.		  
*** 36 Daljnji rad:
Napisati rekurzivnu funkciju za prebrojavanje parnih prirodnih brojeva od 2 do 7.		  
*** 37 Daljnji rad:
Napisati rekurzivnu funkciju za prebrojavanje neparnih prirodnih brojeva od 2 do 7.		  
*** 38 Daljnji rad:
Napisati rekurzivnu funkciju za prebrojavanje prirodnih brojeva od k do n.		  
*** 39 Daljnji rad:
Napisati rekurzivnu funkciju za prebrojavanje parnih prirodnih brojeva od k do n.		  
*** 40 Daljnji rad:
Napisati rekurzivnu funkciju za prebrojavanje parnih prirodnih brojeva od a do b.		  
*** 41 Daljnji rad:
Napisati rekurzivnu funkciju za prebrojavanje neparnih prirodnih brojeva od k do n.		  
*** 42 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje aritmetičke sredine prirodnih brojeva od 4 do 9.		  
*** 43 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje aritmetičke sredine parnih prirodnih brojeva od 4 do 9.		  
*** 44 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje aritmetičke sredine prirodnih brojeva od k do n.		  
*** 45 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje aritmetičke sredine parnih prirodnih brojeva od k do n.		  
*** 46 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje aritmetičke sredine neparnih prirodnih brojeva od k do n.		  
*** 47 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje aritmetičke sredine prirodnih brojeva od a do b..		  
  III Funkcije - Rekurzija - Sabiranje i množenje prirodnih brojeva /FUNCTIONS - RECURSION - SUM AND MULTIPLY/ Rješenja
*** 48 Daljnji rad:
Napisati rekurzivnu funkciju i za ispis sume recipročnih vrijednosti prvih n prirodnih brojeva (harmonijski niz: 1 + 1/2 + 1/3 + ... + 1/n).		  
*** 49 Daljnji rad:
Napisati rekurzivnu funkciju i za ispis sume vrijednosti prvih n brojeva niza: 1/2 + 1/4 + ... + 1/2*n.		  
*** 50 Daljnji rad:
Napisati rekurzivnu funkciju i za ispis sume vrijednosti prvih n brojeva niza: 1/2 + 1/3 + ... + 1/n).		  
*** 51 Daljnji rad:
Napisati program, koristiti rekurziju, za izračunavanje formule: c = n! + m!		  
*** 52 Daljnji rad:
Napisati program, koristiti rekurziju, za izračunavanje formule: c = n! * m!		  
*** 53 Daljnji rad:
Napisati program, koristiti rekurziju, za izračunavanje x=(a!-b!)/c! - funkcija proizvod.		  
*** 54 Daljnji rad:
Napisati program, koristiti rekurziju, za izračunavanje formule:  c=n!/m!(n-m)! sa funkcijom za izračunavanje faktorijela.		  
*** 55 Daljnji rad:
Napisati program, koristiti rekurziju, koji će za učitanu vrijednost n izračunati vrijednost izraza i ispisati: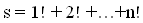
  
*** 56 Daljnji rad:
Napisati program, koristiti rekurziju, za izračunavanje formule: s=1+2!/3+3!/6+...+n!/(1+2+3+...+n) sa funkcijama za izračunavanje faktorijela i zbira prvih k prirodnih brojeva.		  
*** 57 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje formule: s=1+2/2!+6/3!+...+n(n-1)/n! sa funkcijom za izračunavanje faktorijela.		  
*** 58 Daljnji rad:
Napisati rekurzivnu funkciju za izračunavanje najvećeg zajednički djelioca dva učitana prirodna broja. Koristiti Euklidov algoritam.		  
59 Riješiti rekurzijom da li je broj n prost ili složen. C++
*** 60 Daljnji rad:
Napisati rekurzivnu funkciju koja izračunava vrijednost binomnog koeficijenta :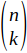
  
  IV Funkcije - Rekurzija - Izdvajanje cifara broja /FUNCTIONS - RECURSION - EXTRACT DIGITS FROM NUMBER/ Rješenja
61 Napisati rekurzivnu funkciju koja računa sumu cifara datog cijelog broja n. C++
*** 62 Daljnji rad:
Napisati rekurzivnu funkciju int suma_parnih(int n) koja računa sumu parnih cifara datog cijelog broja n. 		 
*** 63 Daljnji rad:
Napisati rekurzivnu funkciju int suma_neparnih(int n) koja računa sumu neparnih cifara datog cijelog broja n. 		 
64 Napisati rekurzivnu funkciju int proizvod_cifara(int n) koja računa proizvod cifara datog cijelog broja n. C++
*** 65 Daljnji rad:
Napisati rekurzivnu funkciju int proizvod_parnih(int n) koja računa proizvod parnih cifara datog cijelog broja n. 		 
*** 66 Daljnji rad:
Napisati rekurzivnu funkciju int proizvod_neparnih(int n) koja računa proizvod neparnih cifara datog cijelog broja n. 		 
*** 67 Daljnji rad:
Za dati broj naći sumu parnih i sumu neparnih njegovih cifra, koristiti rekurziju		  
*** 68 Daljnji rad:
Napisati rekurzivnu funkciju int prebroj_cifre(int n) koja računa broj cifara datog cijelog broja n. 		 
*** 69 Daljnji rad:
Napisati rekurzivnu funkciju int broj_parnih(int n) koja računa broj parnih cifara datog cijelog broja n. 		 
*** 70 Daljnji rad:
Napisati rekurzivnu funkciju int broj_neparnih(int n) koja računa broj neparnih cifara datog cijelog broja n. 		 
*** 71 Daljnji rad:
Napisati rekurzivnu funkciju koja obrće cifre datog cijelog broja n. Test primjer:
1234567
7654321		  
*** 72 Daljnji rad:
Napisati rekurzivnu funkciju koja sve cifre datog nenegativnog cijelog broja ispisuje s desna na lijevo. Test primjer:
34567
7 6 5 4 3		  
*** 73 Daljnji rad:
Napisati rekurzivnu funkciju koja sve cifre datog nenegativnog cijelog broja ispisuje s lijeva na desno. 		 
*** 74 Daljnji rad:
Napisati rekurzivne funkcije koja ispisiju dekadne cifre datog cijelog broja, a zatim ispisiju dekadne cifre datog celog broja u obrnutom redoslijedu. Test primjer:
1234567
1 2 3 4 5 6 7
7 6 5 4 3 2 1.		  
*** 75 Daljnji rad:
Napisati rekurzivnu funkciju koja ostavlja parne cifre (izbacuje sve neparne cifre) datog cijelog broja n. Test primjer:
1234567
246.		  
*** 76 Daljnji rad:
Napisati rekurzivnu funkciju koja ostavlja neparne cifre (izbacuje sve parne cifre) datog cijelog broja n. Test primjer:
1234567
1357		  
*** 77 Daljnji rad:
Napisati rekurzivnu funkciju koja poslije svake neparne cifre datog broja dodaje 0.		  
*** 78 Daljnji rad:
Napisati rekurzivnu funkciju koja poslije svake parne cifre datog broja dodaje 0.		  
*** 79 Daljnji rad:
Napisati rekurzivnu funkciju koja ostavlja neparne cifre (izbacuje sve parne cifre) datog cijelog broja n. Te okreće redoslijed formiranog broja. Test primjer:
1234567
7531		  
*** 80 Daljnji rad:
Napisati rekurzivnu funkciju koja ostavlja parne cifre (izbacuje sve neparne cifre) datog cijelog broja n. Te okreće redoslijed formiranog broja.Test primjer:
1234567
642		  
*** 81 Daljnji rad:
Napisati rekurzivnu funkciju int nadji_cifru(int n, int k) koja u datom cijelog broja n nalazi k-tu cifru sdesna. 		 
*** 82 Daljnji rad:
Napisati rekurzivnu funkciju za formiranje novog broja uklanjanjem svih pojavljivanja date cifre c iz datog broja n.		  
*** 83 Daljnji rad:
Napisati rekurzivnu funkciju koja u početnom zapisu broja n izbacuje svaku cifru 3 ispred koje je cifra 2.
Primjer 1:  Primjer 2:  Primjer 3:  Primjer 4:
234         23523       12345       0
24          252         1245        0
  
*** 84 Daljnji rad:
Napisati rekurzivnu funkciju koja u početnom zapisu broja n izbacuje svaku neparnu cifru, ukoliko se ispred te cifre nalazi cifra 2. Napisati program koji testira ovu funkciju, tako što sa standardnog ulaza učitava cio broj x, i na standardni izlaz ispisuje vrijednost funkcije f3(x). U slučaju greške ispisati -1 na standardni izlaz za greške.
Napomena: Zadatak mora biti uradjen rekurzivno. Nije dozvoljeno korišćenje statičkih i globalnih promenljivih, menjanje zaglavlja funkcije i pisanje pomoćnih funkcija.
Primjer 1:  Primjer 2:  Primjer 3:  Primjer 4:
325         23523       12345       0
32          252         1245        0
  
*** 85 Daljnji rad:
Napisati rekurzivnu funkciju void napravi_niz(int* kraj niza, int broj) koja kreira niz cifara datog cijelog broja. Napisati rekurzivnu funkciju void ispisi niz(int* niz, int n) koja ispisuje elemente niza duzine n. Testirati obe funkcije pozivom iz glavog programa.		  
*** 86 Daljnji rad:
Napisati rekurzivnu funkciju koja računa najveću (maksimalnu) vrijednost cifru datog cijelog broja n.		  
*** 87 Daljnji rad:
Napisati rekurzivnu funkciju koja računa najmanju (minimalnu) cifru datog cijelog broja n.		  
  VI Funkcije - Rekurzija - Konverzije brojeva /FUNCTIONS - RECURSION - CONVERSION/ Rješenja
88 Napisati rekurzivnu funkciju void dekadni_binarni(int n) koja konvertuje dekadni u binarni zapis datog cijelog broja. Test primjer:
Dakadni broj: 3456:
Binaran broj: 1101 1000 0000		 C++
*** 89 Daljnji rad:
Napisati rekurzivnu funkciju koja konvertuje dekadni u binarni zapis datog cijelog broja i ispisuje ga inverznom redoslijedu. Test primjer:
Dakadni broj: 23
Binaran broj: 10111
Binaran broj inverzni redoslijed: 11101		  
*** 90 Daljnji rad:
Napisati rekurzivnu funkciju void dekadni_heksa(int x) koja dekadni zapis datog cijelog broja konvertuje u heksadekadni zapis. Test primjer:
Dakadni broj: 3456:
Heksadecimalni broj: D80		  
  VII Funkcije - Rekurzija - Niz /FUNCTIONS - RECURSION - ARRAY/ Rješenja
*** 91 Daljnji rad:
Napisati rekurzivnu funkciju int maksimum_niza(int*niz, int n) koja odreduje maksimum niza cijelih brojeva.		  
*** 92 Daljnji rad:
Napisati rekurzivnu funkciju int minimum_niza(int*niz, int n) koja odreduje minimum niza cijelih brojeva.		  
93 Napisati program sa rekurzijom za ispis prvih n članova Fibonaccievog niza. Član niza se formira od suma prethodna 2 člana ( 0 1 1 2 3 5 8 13...). C++
*** 94 Daljnji rad:
Napišite rekurzivnu funkciju prototipa int F(int n) koja vraća vrijednost funkcije F(n) koja je definirana rekurzivno:
F(n) = 0 - ako je n <= 0
F(n) = F(n-1)+n - ako je n > 0.
(F(0)=0, F(1)=1, F(2)=3...)		  
*** 95 Daljnji rad:
Napišite rekurzivnu funkciju koja ispisuje članove niza po izrazu F(i)=i*(i+1)/2.(članovi niza: 1, 3, 6, 10, ...).		  
*** 96 Daljnji rad:
Napišite rekurzivnu funkciju koja izračunava suma n članove niza po izrazu F(i)=i*(i+1)/2.(članovi niza: 1, 3, 6, 10, ...).		  
*** 97 Daljnji rad:
Napisati rekurzivnu funkciju void obrni_niz(int* a, int n) koja obrće niz brojeva (niz alocirati dinamički). 		 
*** 98 Daljnji rad:
Napisati rekurzivnu funkciju koja formira niz po izrazu M(i+1) = M(i) + maxCifra(M(i)) * minCifra(M(i)), gdje je i u intervalu od 0 do n. Sa tastature učitati n i vrijednost prvog člana niza (prirodni brojevi). Primjer: k = 12, n = 3,
M(i+1) = M(i) + maxCifra(M(i)) * minCifra(M(i))
M(0)= k = 12
M(1)= 12 + 2 * 1 = 14
M(2)= 14 + 4 * 1 = 18
M(3)= 18 + 8 * 1 = 26		  
*** 99 Daljnji rad:
Napisati rekurzivnu funkciju koja formira niz po izrazu M(i+1) = M(i) + maxCifra(M(i)) * minCifra(M(i)), gdje je i u intervalu od 0 do n. Sa tastature učitati n i vrijednost prvog člana niza (prirodni brojevi). Primjer: k = 12, n = 3,
M(i+1) = M(i) + maxCifra(M(i)) * minCifra(M(i))
M(0)= k = 12
M(1)= 12 + 2 * 1 = 14
M(2)= 14 + 4 * 1 = 18
M(3)= 18 + 8 * 1 = 26
Koji član niza je posljednji koji je različit od prethodnog.		  
*** 100 Daljnji rad:
Napisati rekurzivnu funkciju int palindrom(int* a, int n) koja ispituje da li su elementi nekog niza brojeva poredani palindromski (isto od napred i od pozadi). 		 
  VIII Funkcije - Rekurzija - više funkcija Rješenja
*** 130 Daljnji rad:
Napisati rekurzivnu funkciju za upisano n i k sa tasturere. Ispisuju se k znakova sdesna od ukupno n mjesta.		  
131 Napisati program da ispisuje u prvom redu jedno ime a zatim u svakom narednom po jedno ime više.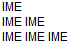
 C++
132 Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7: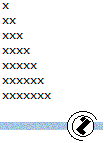
C++
133 Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7: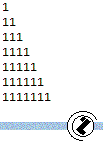
C++
134 Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7: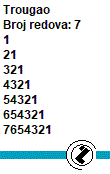
C++
135 Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7:
C++
136 Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7:
C++
*** 137 Daljnji rad:
Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7:
 
138 Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7: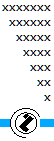
C++
*** 139 Daljnji rad:
Napisati rekurzivnu funkciju void trougao(int n, int trenutna linija) koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7: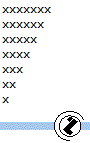
 
140 Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7: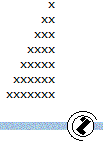
C++
141 Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7:
C++
142 Napisati rekurzivnu funkciju void koja za dato n iscrtava trougao dimenzije n x n. Napr za n=7:
C++
  IX Funkcije - Rekurzija - niske /STRING/ Rješenja
*** 150 Daljnji rad:
Napisati rekurzivnu funkciju koja proverava da li data niska sadrži dati karakter i ukoliko sadrži, vraća mesto gde se taj karakter nalazi (njegovu adresu u okviru niske), a u suprotnom vraća NULL. Testirati funkciju pozivom iz glavnog programa 3 		 
*** 151 Daljnji rad:
Napisati rekurzivnu funkciju koja poredi dve niske i vraca 0 ako su jednake, a 1 ako nisu. Testirati funkciju pozivom iz glavnog programa.		  
*** 152 Daljnji rad:
Napisati rekurzivnu funkciju koja proverava da li je niska s1 podniska niske s2 i ako jeste, vraća pokazivač na mesto gde s1 počinje u s2, a NULL u suprotnom. Nije dozvoljeno korišćenje funkcije strstr. Testirati funkciju pozivom iz glavnog programa. Napomena: Isprobati funkciju strncmp. 		 
*** 153 Daljnji rad:
Napisati rekurzivnu funkciju koja računa koliko puta se niska s1 javlja u okviru niske s2. Testirati funkciju pozivom iz glavnog programa. 4.		  
  X Funkcije - Rekurzija - Kombinovani zadaci /FUNCTIONS - RECURSION/ Rješenja
*** 160 Daljnji rad:
Napisati rekurzivnu funkciju int skalarni_proizvod(int* a, int* b, int n) koja izračunava skalarni proizvod dva data vektora (predstavljena nizovima dužine n). 		 
*** 161 Daljnji rad:
Sa standardnog ulaza se učitava cio broj x, cio broj n (n ≤ 100), a potom i niz od n cijelih brojeva. Napisati rekurzivnu funkciju void f(int a[], int n, int x), koja u nizu a poslavlja na nulu sve parove susednih elementa čiji je zbir (u početnom nizu) jednak x. Rezultujući niz ispisati na standardni izlaz. U slučaju greške ispisati -1 na standardni izlaz za greške.
Napomena: Zadatak mora biti uradjen rekurzivno. Nije dozvoljeno korišćenje statičkih i globalnih promenljivih, menjanje zaglavlja funkcije i pisanje pomoćnih funkcija.
Primjer 1:            Primjer 2:      Primjer 3:      Primjer 4:
3 9                   2 2             5 5             7 8
1 2 7 6 0 3 2 1 4     1 1             8 2 3 2 9       1 5 2 6 3 4 3 9
0 0 7 6 0 0 0 0 4     0 0             8 0 0 0 9       1 0 0 6 0 0 0 9 2
  
*** 162 Daljnji rad:
Napisati rekurzivnu funkciju void f3(int *a, int na) koja u početnom nizu a, duzine na, smanjuje vrijednost broja za 1 ukoliko je on paran, i nakon njega se nalazi paran broj. Kreirati program koji testira ovu funkciju, tako što sa standardnog ulaza učitava broj na(0 ≤ na ≤ 1000), zatim vrijednosti niza a, i na standardni izlaz ispisuje vrijednosti izmenjenog niza. U slučaju greške ispisati -1 na standardni izlaz za greške.
Napomena: Zadatak mora biti uradjen rekurzivno. Napomena: Zadatak mora biti uradjen rekurzivno. Nije dozvoljeno korišćenje statičkih i globalnih promenljivih, menjanje zaglavlja funkcije i pisanje pomoćnih funkcija. 
Primjer 1:             Primjer 2:    Primjer 3:               Primjer 4:
10                     5             10                       -1
2 2 5 7 6 8 4 3 2 1    1 2 2 2 1     4 4 6 6 6 6 8 8 10 10
1 2 5 7 5 7 4 3 2 1    1 1 1 2 1     3 3 5 5 5 5 7 7 9 10     -1
  
*** 163 Daljnji rad:
Napisati rekurzivnu funkciju void f3(int *a, int na, int suma prethodnih) koja u u nizu a, dužine na, postavlja vrijednost svakog broja na 0 ukoliko je veći od sume prethodnih brojeva u nizu. Napisati program koji testira ovu funkciju, tako što sa standardnog ulaza učitava broj na, zatim vrijednosti niza a, i na standardni izlaz ispisuje izmenjeni niz. U slučaju greške ispisati -1 na standardni izlaz za greške.
Napomena: Zadatak mora biti uradjen rekurzivno. Nije dozvoljeno korišćenje statičkih i globalnih promenljivih, menjanje zaglavlja funkcije i pisanje pomoćnih funkcija. 
Primjer 1:             Primjer 2:    Primjer 3:      Primjer 4:
10                     5             2               -1
2 2 5 7 6 25 4 3 2 1   1 2 4 12 9    1 1
0 2 0 7 6 0 4 3 2 1    0 0 0 0 9     0 1             -1
 
*** 164 Daljnji rad:
Sa standardnog ulaza se učitava cio broj n(n ≤ 100), a potom i niz od n cijelih brojeva. Napisati rekurzivnu funkciju void f(int a[], int n) koja u nizu a postavlja na nulu sve elemente koji su (u početnom nizu) jednaki zbiru svojih suseda. Rezultujući niz ispisati na standardni izlaz. U slučaju greške ispisati -1 na standardni izlaz za greške.
Napomena: Zadatak mora biti uradjen rekurzivno. Nije dozvoljeno korišćenje statičkih i globalnih promenljivih, menjanje zaglavlja funkcije i pisanje pomoćnih funkcija. 
Primjer 1:     Primjer 2:    Primjer 3:     Primjer 4:
6              5             2              6
1 4 3 6 3 3    1 0 3 3 0     1 1            1 2 1 1 3 2
1 0 3 0 3 3    1 0 0 0 0     1 1            1 0 1 1 0 2
 

    abc Algoritmi    abc BASIC    abc Turbo Pascal    abc C++    abc Java    abc C    abc Python    abc Dev-Pascal    Index