abc Matlab - elektronski priručnik
III dio Matematika u Matlabu - 3.1. Linearna algebra

3.1.2. Sistemi linearnih jednačina
3.1.2.5. Predeterminisani sistemi

Ovaj primjer pokazuje kako se predeterminisani sistemi često sreću u različitim vrstama uklapanja (tzv. fitovanja) krivih u eksperimentalne podatke.

Neka veličina, y, je mjerena za nekoliko različitih vrijednosti vremena, t, pa su dobijene sljedeće opservacije. Možemo unijeti podatke i vidjeti ih u tabeli pomoću sljedećih naredbi.

t = [0 .3 .8 1.1 1.6 2.3]';
y = [.82 .72 .63 .60 .55 .50]';
B = table(t,y)

B =
      t           y
   ___      ____
      0       0.82
   0.3       0.72
   0.8       0.63
   1.1         0.6
   1.6       0.55
   2.3         0.5

Pokušajmo modelovati podatke sa eksponencijalnom funkcijom raspada

Prethodna jednačina kaže da vektor y treba biti aproksimiran linearnom kombinacijom dva druga vektora. Jedan je konstantni vektor koji sadrži sve jedinice, a drugi je vektor sa komponentama exp(-t). Nepoznati koeficijenti,  i , mogu se izračunati pomoću fitovanja najmanjih kvadrata, što minimizira sumu kvadrata devijacija podataka iz modela. Postoji šest jednačina sa dve nepoznate, predstavljenih sa 6-sa-2 matricom.

E = [ones(size(t)) exp(-t)]

E =
     1.0000             1.0000
     1.0000             0.7408
     1.0000             0.4493
     1.0000             0.3329
     1.0000             0.2019
     1.0000             0.1003

Koristimo backslash operator da dobijemo rješenje najmanjih kvadrata.

c = E\y

c =
          0.4760
          0.3413

Drugim riječima, fitovanje najmanjih kvadrata u podatke je:

Sljedeće naredbe izračunavaju model po regularno razmaknutim inkrementima od t, a onda crtaju rezultat zajedno sa izvornim podacima:

T = (0:0.1:2.5)';
Y = [ones(size(T)) exp(-T)]*c;
plot(T,Y,'-',t,y,'o')

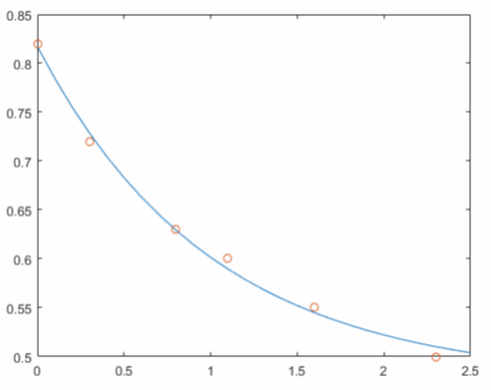
E*c nije tačno jednako y, ali razlika može sigurno biti manja od grešaka mjerenja u izvornim podacima.

Pravougaona matrica A je nepotpunog ranga ako nema linearno nezavisne kolone. Ako je A nepotpunog ranga, rješenje najmanjih kvadrata za AX = B nije jedinstveno. Operator backslash, A\B, izdaje upozorenje ako je A nepotpunog ranga i proizvodi rješenje najmanjih kvadrata ako sistem nema rješenja i osnovno rješenje ako sistem ima beskonačno mnogo rješenja.

Sistemi linearnih jednačina - Kvadratni sistemi - Rješenja najmanjih kvadrata    <    Index    >    Sistemi linearnih jednačina - Poddeterminisani sistemi